문제를 간단히 설명하자면,
n개의 입력값을 받는데, 회의의 시작 시간과 종료시간으로 구성되어 있다. 주
회의를 가능한 많이 진행하고자 한다면, 최대 몇 개의 회의가 진행될 것인가 이다.
뭔가 OS 시간에 배운 scheduling 알고리즘 중에서도 비슷한 게 있었던 것 같다.. 물론 cpu scheduling의 경우엔 중간에 가로채는 것도 가능하고 하니깐 조금은 다른 방향성을 띄게 될 것이다. 모든 프로세스의 시간을 다 알고 있는 것도 아니고,,,
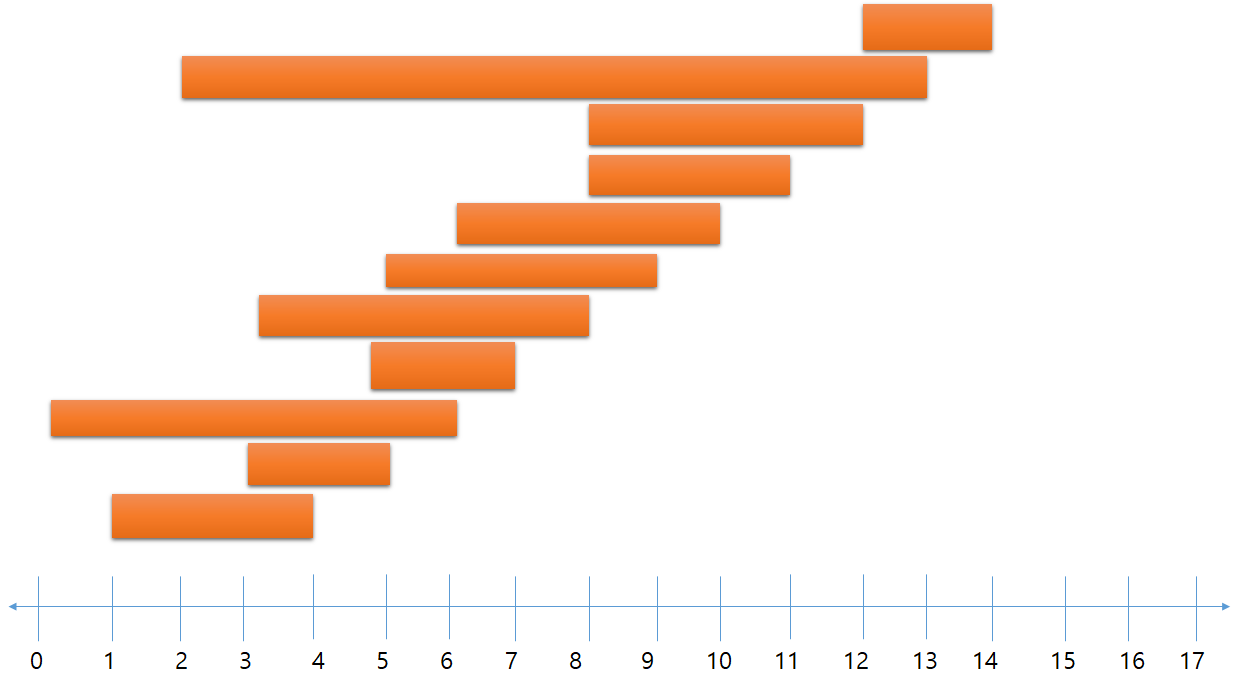
예제로 나와있는 입력값을 도식화 하면 다음과 같다.


주황 막대기는 회의 시간을 나타낸다. 수직으로 내려와 수직선과 만나는 곳에서 시작 시간과 종료 시간을 유추해볼 수 있다. 결국 저 주황 막대들이 겹치지 않게 가장 많이 고르는 방법을 찾는 것이다. 그리고 그 때 주황 막대기의 개수가 곧 출력값이 될 것이다.
이 문제는 그리디 알고리즘(greedy algorithm, 탐욕법) 분류에 들어가 있지만, 문제를 푸는 키(key)는 정렬이라 생각한다. 물론 탐욕법과 관련한 최적 조건을 구하는 것도 중요하다.
우선 탐욕법에 대해 잠깐 설명하자면, 전체를 고려하지 않고 특정 시점에서 최선의 선택을 하는 것이다.
예를 들어 첫 번째 회의로 (시작시간, 종료시간)이 (1,4)인 회의를 골랐다면, 4시부터 시작하는 회의 중 최선의 선택을 하는 것이다. 즉, 각 시점에서의 최선의 선택의 기준이 무엇인가가 중요하다.
이렇게 풀면 좋은 점은 특정 문제들에 대해서 최적의 해를 빨리(모든 경우를 고려하지 않기에) 구할 수 있다는 것이다.
그럼 위 문제에서 최선의 선택 기준은 무엇일까? 그건 바로 현 시점에서 가장 일찍 끝나는 회의이다. 회의가 일찍 끝나야 회의를 진행할 수 있는 시간이 많이 남기 때문이다. 따라서 회의를 고르되 일찍 끝나는 순서대로 담는다. 여기서 하나 더 고려할 점이, 첫 번째 회의는 상관 없지만, 두 번째 회의부터는 이전 회의가 끝난 후부터 진행되는 회의여야 한다는 제약이 붙는다.
앞에서 정렬이 중요하다 했는데, 정렬은 왜 중요한가? 정렬을 한 번 해주면, loop를 여러 번 돌지 않고 한 번의 loop만에 해결할 수 있다. (필자는 처음에 정렬 없이 loop를 여러 번 돌았다가 번번히 시간초과에 걸렸다..)
정렬 기준은 1) 종료시간, 2) 시작시간 으로 모두 오름차순이다.
정렬을 하면 다음과 같은 결과가 된다.
이제 한 번 실제 알고리즘이 어떻게 동작하는 지 살펴보자.
우선 가장 먼저 끝나는 1번째 회의를 고른다.

다음 회의는 첫 번째 회의가 끝난 후 시작되어야 하며 남은 회의 중 가장 먼저 끝나야 한다.

다음 회의도 마찬가지로 진행한다.

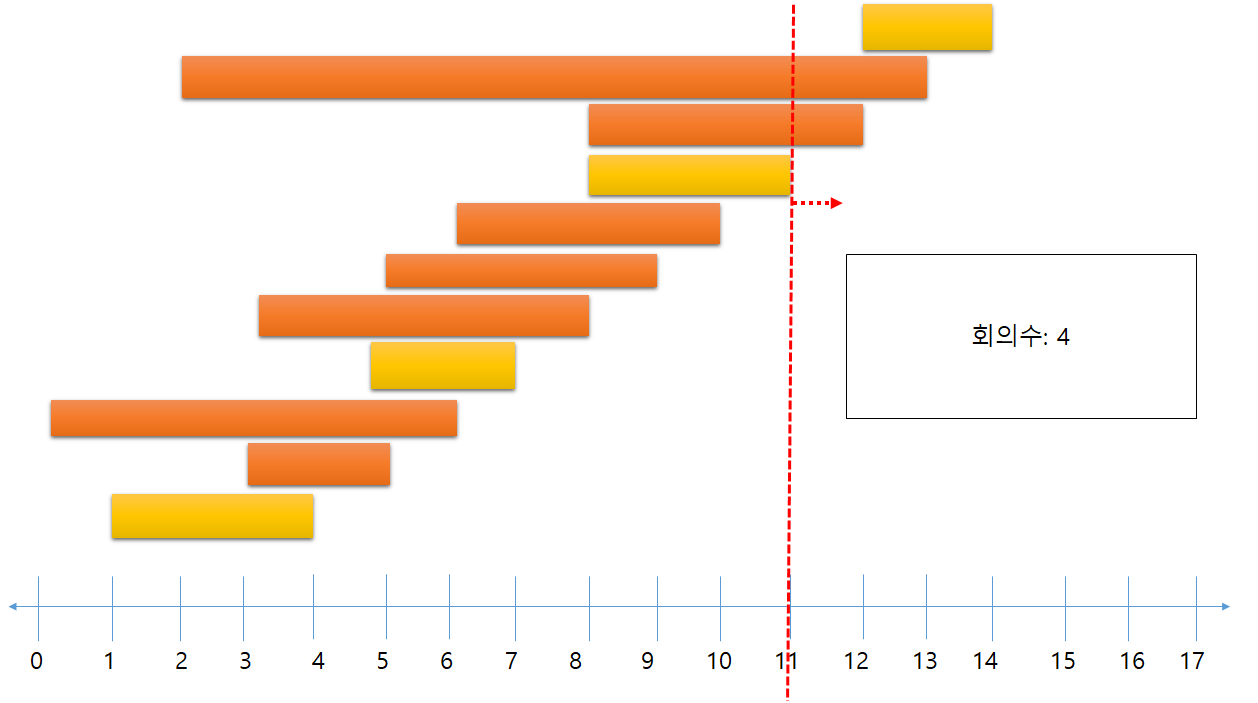
이렇게 진행하면 최대 4개의 회의가 진행될 수 있음을 알 수 있다.
정렬에 있어서 왜 2번째 기준으로 시작 시간을 굳이 주었냐 하면, 시작 시간에 따라 정렬되지 않은 상태이고, 종료시간 기준으로만 정렬되어 있다면, 다음과 같은 상황이 나타날 수 있다.

처음에 짠 알고리즘에 따르면(시작 시간에 따른 정렬도 포함) (5,9), (9,9)가 진행되어 2개가 들어가야 하지만, 위와 같이 정렬된 경우, (9, 9)회의만 진행될 수 있다. 따라서 1기준으로 종료시간을 잡고 2기준으로 시작 시간도 잡아주어야 한다.
다음은 파이썬 소스코드이다.
#1931 회의실 배정 python
n = int(input())
ls = []
cnt = 1
for i in range(n):
s, e = map(int, input().split()) # start, end time
ls.append((s, e))
ls = sorted(ls, key = lambda x : (x[1], x[0]))
sum_min = ls[0][1]
for i in range(1, len(ls)):
if ls[i][0]>=sum_min:
sum_min = ls[i][1]
cnt+=1
print(cnt)
'컴퓨터' 카테고리의 다른 글
| [데이터 베이스] 함수적 종속성(Functional dependency) (0) | 2020.06.13 |
|---|---|
| [데이터 베이스] 관계형 데이터베이스 매핑(Mapping) (0) | 2020.06.12 |
| [컴퓨터 구조] CPU time (2) | 2020.06.09 |
| [알고리즘] 백준. #1904 01타일 (0) | 2020.06.08 |
| [알고리즘] 백준. 2748, 1003 피보나치(동적 계획법) (0) | 2020.06.06 |



댓글